Операции над событиями. Теория вероятностей
Пересечение событий
Пусть есть события A и B, у каждого события есть набор элементарных исходов. Пересечением событий A и B называют то событие, в результате которого произошло и событие A и событие B, то есть случился некоторый элементарный исход, который одновременно принадлежит и событию A и событию B.
События не пересекаются
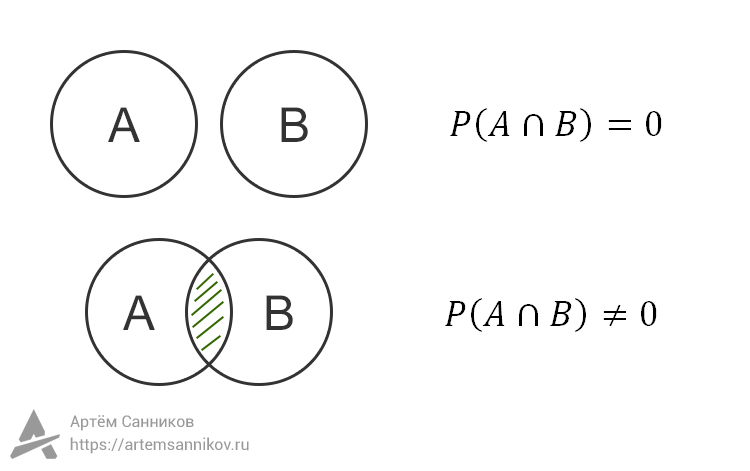
Если у событий A и B нет пересечения (отсутствует элементарный исход), то такая вероятность равна нулю.
События пересекаются
Если события A и B пересекаются (имеют некоторое общее количество элементарных исходов), то вероятность этого пересечения нельзя рассчитать по какой-то универсальной формуле. Эту вероятность нужно подсчитывать, рассматривая общие элементарные исходы.
Объединение событий
Объединением событий A и B называют те события, в результате которых произошло или событие A, или событие B, то есть хотя бы одно из двух.
События не пересекаются
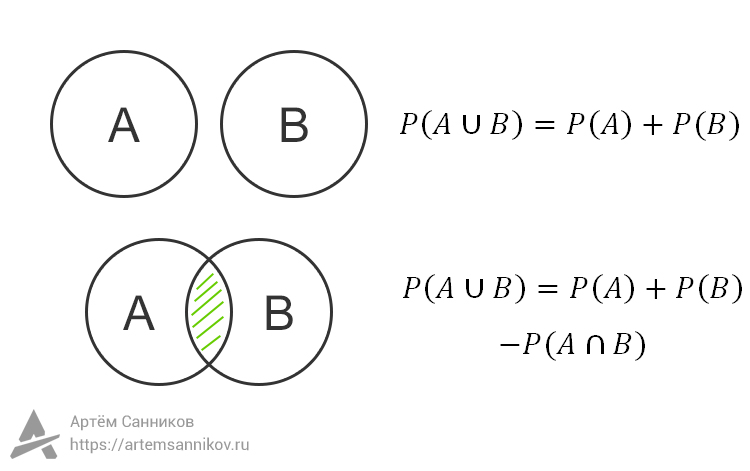
Если события A и B не пересекаются, то вероятность их объединения окажется равной = вероятность события P(A) + вероятность события P(B).
События пересекаются
Если события A и B пересекаются, то есть у них есть общие элементарные исходы, то вероятность их объединения окажется равной = вероятность события P(A) + вероятность события P(B) — вероятность пересечения событий P(A ∩ B)
Независимые события
События A и B независимы, если наступление одного события не влияет на другое событие.
Практический пример
Будем рассматривать пример с игральным кубиком, для простоты и анализа нашего эксперимента введём следующие обозначения:
- 1 очко = ω1;
- 2 очка = ω2;
- 3 очка = ω3;
- 4 очка = ω4;
- 5 очков = ω5;
- 6 очков = ω6.
Событие A: выпало > 3 очков
Событие B: выпало нечетное число очков
Чтобы приступить к решению задачи выполняем анализ событий.
Анализ события A: этому событию соответствует три элементарных исхода { ω4, ω5, ω6}
Анализ события B: этому событию соответствует три элементарных исхода{ ω1, ω3, ω5}
После анализа событий приступаем к пошаговому решению.
Рассмотрим теперь пересечение события A и B, то есть у нас должно выпасть > 3 очков и при этом число должно быть нечётное. В этом случае у нас есть один элементарный исход: { ω5}.
Отсюда мы можем посчитать вероятность этого события:
- n – элементарный исход, который удовлетворяет нашим условиям;
- N – общее количество исходов.
Далее рассмотрим объединение событий A и B. В данном случае у нас будет следующий набор элементарных условий { ω1, ω3, ω4, ω5, ω6}
Обратите внимание: у нас отсутствует ω2, так как этот исход не фигурирует ни в событии A, ни в событии B.
Поэтому мы можем сказать, что вероятность объединения в этом случае будет:
По факту мы решили задачу, но мы можем её решить намного быстрее, если воспользуемся формулой, которую изучили ранее:
- Вероятность P(A) – выпало > 3 очков
- Вероятность P(B) – выпало нечётное число
- Вероятность P(A ∩ B) – пересечение событий A и B
Метки: Математика, Теория вероятностей.







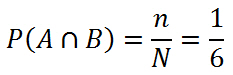
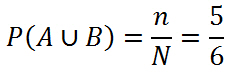
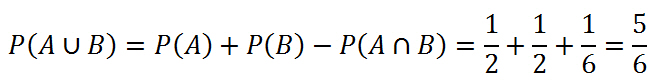
Большое спасибо за статью! А это и есть операции над событиями? Пересечение, объединение и независимость?
Да, все верно.
в последнем примере ошиблись знаком, д. б. минус
Имеете ввиду пример — объединение событий a и b?