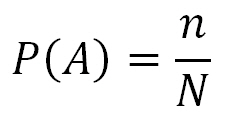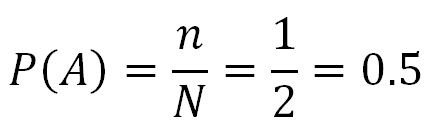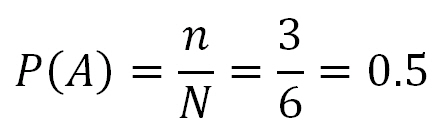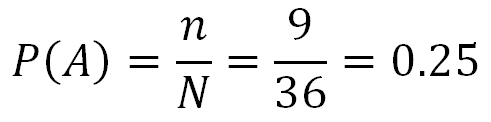Погружение в базы данных Oracle
Данная книга является руководством для начинающих специалистов в области анализа и обработки данных. В книге рассматривается язык SQL и его процедурное расширение PL/SQL от компании Oracle.
SQL без слёз
Цель книги заключается в том, чтобы научить любого человека работать с реляционными базами данных и получать из них необходимую информацию посредством выполнения SQL-запросов.
Классическая вероятность. Теория вероятностей
Классическая вероятность
Классическая вероятность подразумевает, что все исходы нашего эксперимента равновероятные (вероятность каждого 1/N). Мы не можем сказать, что событие 1 будет наступать с больней вероятностью чем событие 2, или наоборот.
Формула вычисления классической вероятности
- P — классическая вероятность;
- n — количество исходов интересующего нас события;
- N — общее количество исходов в данном эксперименте.
Эксперимент с симметричной монетой
Формулировка эксперимента: подбрасываем симметричную монету (орёл и решка).
Анализ: в нашем случае выпадет либо орёл, либо решка, значит у нас есть 2 исхода события. Основываясь на общем количестве исходов в эксперименте, можем посчитать вероятность по классической формуле:
Эксперимент с игральной костью (кубиком)
Игральная кость представляет собой куб с 6 плоскостями на которых нанесены значения 1, 2, 3, 4, 5 и 6, а это значит что у нас есть 6 возможных исходов. Давайте разберём на простых примерах задачу с игральным кубиком.
Вероятность нечётного числа на кубике:
Всего возможных исходов будет N=6 (числа на кубике 1,2,3,4,5 и 6), а событий которые удовлетворяют нашему условию будет n=3 (то есть все нечётные числа 1,3 и 5).
Вероятность выпадения двух нечётных чисел подряд:
Сначала запишем все элементарные исходы, которые могут возникнуть при двух бросках подряд. Для этого сделаем таблицу и отобразим 6 колонок (так как у куба 6 плоскостей со значениями), в которых будет отображаться вероятность выпадания чисел.
Сразу введём обозначения для событий, чтобы не было путаницы:
- ω1 = 1 очко;
- ω2 = 2 очка;
- ω3 = 3 очка;
- ω4 = 4 очка;
- ω5 = 5 очков;
- ω6 = 6 очков;
Логика при составлении таблицы: При первом броске значение у нас остаётся одинаковым, при повторном броске значение меняется.
Всего возможных исходов N=36
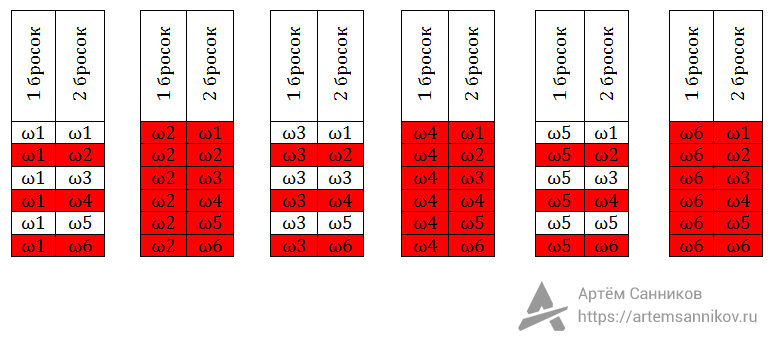
Сейчас мы уберём события, которые не удовлетворяют нашему условию, а именно — вероятность выпадения двух нечётных чисел подряд. Пройдёмся по каждому столбику слева направо:
- 1 столбик: убираем все вероятности (ω1-ω2, ω1-ω4, ω1-ω6), в которых есть чётные числа;
- 2 столбик: убираем полностью, так как при первом броске у нас выпадет ω2 (чётное число);
- 3 столбик: убираем все вероятности (ω3-ω2, ω3-ω4, ω3-ω6), в которых есть чётные числа;
- 4 столбик: убираем полностью, так как при первом броске у нас выпадет ω4 (чётное число);
- 5 столбик: убираем все вероятности (ω5-ω2, ω5-ω4, ω5-ω6), в которых есть чётные числа;
- 6 столбик: убираем полностью, так как при первом броске у нас выпадет ω6 (чётное число);
Всего возможных событий, который удовлетворяют нашему условию осталось n=9
После того, как мы вычислили все возможные исходы N и события n, которые удовлетворяют нашему условию, можно найти вероятность P(A).
Метки: Математика, Теория вероятностей.
