Погружение в базы данных Oracle
Данная книга является руководством для начинающих специалистов в области анализа и обработки данных. В книге рассматривается язык SQL и его процедурное расширение PL/SQL от компании Oracle.
SQL без слёз
Цель книги заключается в том, чтобы научить любого человека работать с реляционными базами данных и получать из них необходимую информацию посредством выполнения SQL-запросов.
Основные понятия теории вероятностей
Что такое теория вероятностей?
Теория вероятностей (тер.вер) — раздел математики, который занимается изучением случайных событий, случайных величин, их свойства и операции над ними.
Теория вероятностей встречается в нашей жизни почти каждый день, вот несколько самых распространённых примеров с которыми сталкивался каждый: бросок монеты, игральные кубики и т.д.
Вероятность
Вероятность — это степень уверенности в том, что то или иное событие произойдёт.
Результат каждого отдельного процесса предсказать невозможно (какие бы сложные расчёты не использовались). Однако, теория вероятностей использует закономерности и соотношения между случайными процессами для того, чтобы в сложных реальных ситуациях принимать обоснованные решения.
В качестве закрепления понятия вероятность, рассмотрим эксперимент.
Формулировка эксперимента: Когда мы подбрасываем монету, мы не можем предсказать исход события, так как события равновероятное, но мы знаем, что это событие произойдёт (выпадет либо орёл, либо решка).
Но есть ещё и третий вариант — монета встанет на ребро, этот вариант мы тоже не можем предсказать (но он имеет место быть).
Элементарный исход
Элементарный исход — это всего лишь один из возможных результатов какого-то эксперимента.
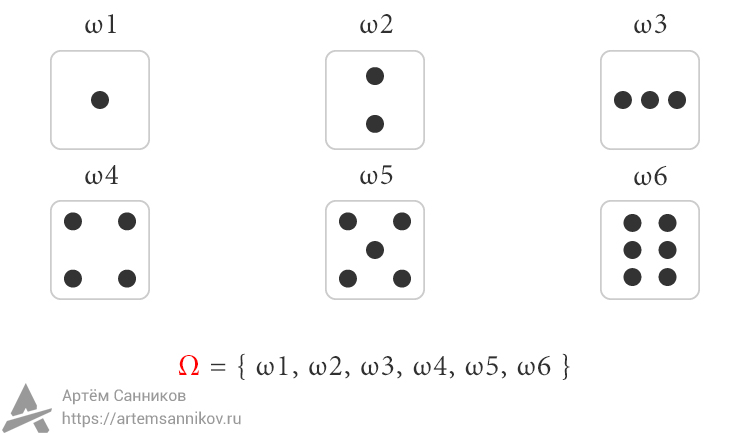
Формулировка эксперимента: Бросок игральной кости (кубика). В результате эксперимента мы можем получить 1 из 6 возможных исходов, то есть когда мы бросаем кубик он может упасть на поверхность одной из своих граней (нам может выпасть значение 1, 2, 3, 4, 5 или 6).
Соответственно мы можем назвать каждый исход какой-нибудь буквой, например ω. Итого у нас получится ω1, ω2, ω3, ω4, ω5 и ω6 (смотрите рисунок ниже). Все эти шесть исходов вместе составляют так называемое — вероятностное пространство (Ω).
Вероятностное пространство (Ω) — все возможные исходы события.
Событие
Событие — набор элементарных возможных исходов в эксперименте.
Чтобы было понятно о чём идёт речь, рассмотрим предыдущий эксперимент с игральной костью (кубик). В нашем случае мы можем получить следующие исходы (запишем в следующем формате Событие -> Исход):
- выпало 1 очко -> {ω1};
- выпало нечётное число очков -> {ω1, ω3, ω5};
- выпало 5 или 6 очков -> {ω5, ω6};
- невозможное событие (кубик упал на ребро) -> { }, оставляем множество пустым;
- достоверное событие -> {ω1, ω2, ω3, ω4, ω5, ω6}.
Метки: Математика, Теория вероятностей.
